一)什么是无理数化简?为什么要化简?

如上面的几个二次根式的化简,就是通过无理数的运算把算式写成最简形式。为什么要这样做呢?因为简洁一致的表达才是数学的语言,一方面更容易让人理解,二方面容易比较相同或类似的结果。就像你们在学分数时,8/64=1/8,老师一定要写成既约分数的形式一样。
二)要化简成什么样子?
化简的标准:
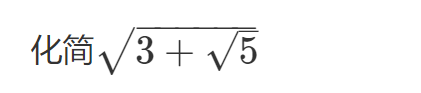
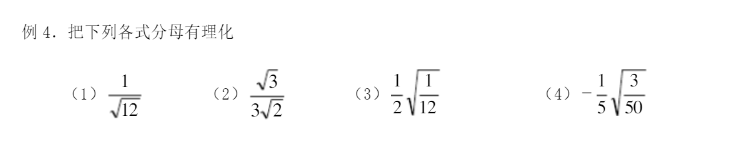

三)根式内整数分解开方
1)素数与算数基本定理
你该问啦,化简就化简呗,这和什么素数有啥关系。
质数又称素数(prime number)一个大于1的自然数,除了1和它自身外,不能被其他自然数整除的数叫做质数;否则称为合数(规定1既不是质数也不是合数)。
根据它的定义就知道,如果从乘除的角度来构成全体自然数,那么素数就是最基础的数字,是骨架。你在分数约分的时候,也会用到这一点。那个时候讲的是以下几个定义:
可以回想一下,当时都是用素数或素数的乘积来运算的,包括你现在开根号也要把根号内的数字表示成素数乘积的方式。为啥呢?当当当当》》》》》》
算数基本定理
又称为正整数的唯一分解定理,每个大于1的自然数可以写成质因子按大小排列乘积的形式,并且写法有且仅有一种。(证明自己查资料研究)

(更为严谨的定义)
啥意思呢?就是你在分解根式内的整数的时候,不管你咋除,最后的结构都一样!!!只要你按因子大小顺序排,最后肯定有且只有一种形式。(这让我想起了玩斗牛的一个笑话,一个朋友说相同的五张牌,不同的二三配合就可以出不同的牛,我们都笑晕了)。一听基本定理就很牛吧,这个定理是由欧几里得提出并证明,最后由高斯拓展为代数基本定理。
2)整数的因数分解
这是整数的因数分解的基础,举个例子:1250=2*5^4 (后面的符号代表5的四次方)
(我还发现了个好玩的网站可以帮你完成因数分解,还有很多好玩的数学工具。
https://zh.numberempire.com/)
根据这个因数分解的结果,就可以把可以开方的因数运算,从而得到简化的结果。
3)根式的基本运算法则
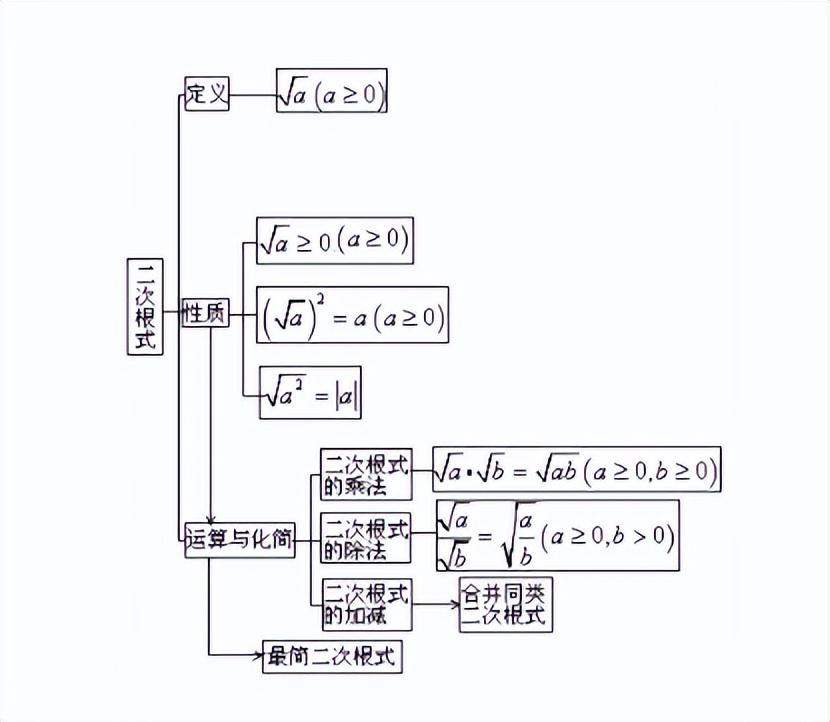
4)一个隐含的基础
整数的因数分解是数学上一个重大的问题,这个用在所有的银行及网络系统加密。没想到吧!你会感觉这有什么难的。原因是给出一个很大的数字,比如128位的数,要找到其质数因子分解的过程非常耗时和需要巨大的计算机算力。
你们做这个题目当让就不用啦,但是起码要掌握:
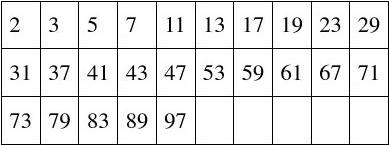
100以内的素数表

10或更多的平方与立方表
这样你就可以快速进行因式分解了。
比如112=16*7 那么根号112就可以快速分解为4根号7,用得多了你会越来越熟练。
总结一下:
1)根式运算与化简是为了形式简洁
2)化简有一定的标准
3)最基础的就是根式内部分解运算开方
4)整数因数分解的基础是算数基本定理
5)掌握了素数表、平方表和立方表可以帮助你快速分解因数